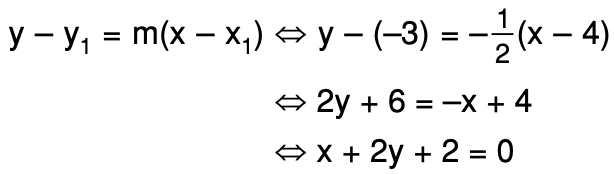kali ini kita akan membahas soal berikut nya…
Tentukan garis yang sejajar dengan x + 2y – 5 = 0 yang membagi lingkaran x2 + y2 – 8x + 6y – 20 = 0 menjadi dua bagian yang sama!
Jawab:
g: x + 2y – 5 = 0 maka mg = – ½
karena sejajar, maka garis yang membagi dua lingkaran itu juga memiliki gradien yang sama, yaitu m = mg = – ½.
x2 + y2 – 8x + 6y – 20 = 0
x2 – 8x + 16 + y2 + 6y + 9 = 20 + 16 + 9
(x – 4)2 + (y + 3)2 = 45
Pusat: (4, -3)
Garis membagi dua lingkaran, jika garis tersebut melalui titik pusat.
Persamaan garis yang melalui titik (4, -3) dan bergradien m = – ½
Jadi garis yang dimaksud adalah x + 2y + 2 = 0
—————-#—————-
Jangan lupa komentar & sarannya
Email: [email protected]
Kunjungi terus: mastah.my.id OK! 😁
[ad_2]